[ML/데이터 전처리] Feature Selection - Filter
- -
Feature Selection(특징 선택): 모델을 구성하기 위한 Feature을 선택하는 과정
고차원, 즉 피처가 많을 수록 데이터 포인트 간의 거리가 기하급수적으로 멀어진다. 이 Curse of Dimensionality(차원의 저주)가 일어나는데 해당 데이터로 학습을 시켰을 때 예측에서 정확도가 떨어진다.
복잡도를 감소시켜 모델의 성능을 향상시키고 처리속도를 증가시키기 위해 하는 방법 중에 하나가 Feature Select이다.
특징 선택 알고리즘은 크게 Filter, Wrapper, Embedded 3가지로 구분한다.

이 세가지 방법론을 하나만 선택해서 사용한다기보다는 같이 사용한다. (ex. Wrapper method를 사용하기 전에 Filter method를 사용)
Filter
데이터 전처리 단계에서 통계적 측정 방법을 사용하여 적절한 Feature를 선택하는 방식이다. 측정된 지표를 활용해 모델에서 관련없는 feature나 중복 등을 filtering한다.
해당 방법은 계산 시간이 짧고 데이터에 overfit되지 않는다는 장점이 있다.
Filter에서 사용하는 방법론
- Information Gain: 데이터셋을 변환하는 동안 엔트로피의 감소를 결정. 목표 변수에 대한 각 변수의 information gain을 계산해 filter에 이용
- Chi-square Test: 카이제곱 검정은 범주형 변수 간의 관계를 파악하는 기법. 각 특징과 대상 변수 간의 카이제곱값을 계산해 카이제곱값이 가장 좋은 특징의 개수를 선택
- Fisher's Score: feature select에서 널리 사용되는 supervised 기법. 피셔 기준에 따른 변수의 순위를 내림차순으로 반환한다. 피셔 점수가 큰 변수를 선택하는 방식으로 사용
- Missing Value Ratio: 결측치 비율을 구하는 공식을 통해 임계값을 초과하는 변수는 삭제(공식: 각 열의 결측치 수를 총 관측치 수로 나눈 값)
- corelation coefficient: 상관관계 분석을 통해 상관관계가 높은 쌍을 찾아냄. 상관관계가 높은 열을 삭제함.
Information Gain
Information Gain: Information entropy의 차이로 계산되는 수치로 대표적으로 Decision Tree에서 사용된다.
Information Gain에 대한 자세한 포스팅은 다음에 하도록 하겠다. 간단하게 Entropy는 heterogeneous한 정도, 즉 혼잡도를 의미한다는 것과 Information Gain이 최대화 되는 변수를 선택하는 방법으로 filtering한다는 것만 알아두자.
feature select에서는 IG를 Mutual Information이라고 부른다. 이는 거의 동일한 용어로 사용되며 실제로도 거의 같은 개념이다. 이 둘의 관계는 marginal probability distributions (mutual information)의 차이가 클수록 information gain이 커지는 것으로 이해할 수 있다.
- 데이터 집합에 대한 transform의 효과: Information Gain
- 변수 간 종속성 계산: Mutual Information
즉 Mutual Information은 두 개의 변수를 대상으로 산정되는 것으로 KL divergence로도 계산할 수 있다.
$$ I(X ; Y) = H(X) – H(X | Y) $$
$$ I(X ; Y) = KL(p(X, Y) || p(X) * p(Y)) $$
다른 개별 변수의 변화로 인해 target 변수의 불확실성의 감소량을 계산하는 것이다.
이 방법의 장점은 속도가 빠르다는 점과 모델 중립적이므로 다양한 종류의 ML 모델에 적용할 수 있다는 점이다.
Code
다음은 예시 코드이다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("") # csv파일 불러오기
# X와 y 잡아주기
X = df.iloc[:, :-1]
y = df.iloc[:, -1]sklearn의 mutual_info_classif를 불러온다. 이 라이브러리는 k-nn에서 엔트로피 추정을 기반으로 하는 비모수적 방법에 의존한다.
sklearn.feature_selection.mutual_info_classif(X, y, *, discrete_features='auto', n_neighbors=3, copy=True, random_state=None)
여기서 n_neighbors는 연속 변수에 대한 MI 추정에 사용할 이웃 개수를 의미함
# sklearn의 mutual information 계산해주는 라이브러리를 불러옴
from sklearn.feature_selection import mutual_info_classif as MIC
mutual_info = MIC(X,y)
mutual_info = pd.Series(mutual_info)
mutual_info.index = X.columns
mutual_info.sort_values(ascending = False)
mutual_info.sort_values(ascending=False).plot.bar(figsize=(12, 6))

from sklearn.feature_selection import SelectKBest
# 변수 3가지 선택
sel_3_cols = SelectKBest(MIC, k=3)
sel_3_cols.fit(X, y)
X.columns[sel_3_cols.get_support()]
변수를 3가지로 선택한 건 특별한 의미가 없다. 따라서 데이터에 따라 필요한 변수의 개수를 잘 선정해야한다. 여기서는 개수를 정해서 사용했지만 mutual_info_classif의 점수에 따라 임계값을 정해 사용하는 방법도 있다.
Chi-square Test
Chi-square Test(카이제곱 테스트): 카이제곱 분포에 기초한 통계적 방법, 관찰된 빈도가 기대 빈도와 통계적으로 다른지를 판단하는 검증방법.
이에 대해서 설명하려면 카이제곱 분포에 대해서도 설명을 해야하나 이것까지 설명하면 포스팅이 너무 길어지니 이것 역시 차후 다른 포스팅에서 다뤄보도록 하겠다.
두 변수의 데이터가 주어지면 관찰된 카운트 O와 예상 카운트 E를 구할 수 있다. 카이제곱은 예상 카운트 E와 관찰된 카운트 O가 서로 어떻게 편차하는지를 측정하는 방식으로 변수의 연관성을 측정한다. 또, 이 방법은 category feature에만 사용 가능하다.

두 feature가 독립적인 경우 O가 E에 가깝기 때문에 카이제곱 값이 작아진다. 즉 카이제곱 값이 높으면 독립적이지 않다는 것을 의미한다. 따라서 카이제곱 값이 높은 변수를 선택하는 것으로 feature select가 이루어진다.(target 변수와 연관이 높음)
카이제곱 테스트를 수행하는 단계는 다음과 같다
- 가설을 정의한다
- 귀무가설(H0): 두 변수는 독립적이다.
- 대립가설 (H1): 두 변수는 독립적이지 않다.
- 조건부 테이블을 작성한다
- 예상값을 구한다
- 카이제곱 통계를 계산한다
- 귀무가설을 accept하거나 reject한다
카이제곱 값이 오차 영역에 속하면 귀무 가설을 거부한다는 것만 알아두자. 자세한 설명은 이후 카이제곱 분포에서 하도록 하겠다.
code
import numpy as numpy
import pandas as pd
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
df = pd.read_csv("Transformed Data Set - Sheet1.csv")
# 범주형 변수 인코딩
label_encoder = LabelEncoder()
df['Favorite Color'] = label_encoder.fit_transform(df['Favorite Color'])
df['Favorite Music Genre'] = label_encoder.fit_transform(df['Favorite Music Genre'])
df['Favorite Beverage'] = label_encoder.fit_transform(df['Favorite Beverage'])
df['Favorite Soft Drink'] = label_encoder.fit_transform(df['Favorite Soft Drink'])
df['Gender'] = label_encoder.fit_transform(df['Gender'])데이터를 불러와주고, 범주형 변수를 인코딩해준다.
from sklearn.feature_selection import chi2
X = df.drop('Gender',axis=1)
y = df['Gender']
chi_scores = chi2(X,y)sklearn.feature_selection.chi2(X, y)
라이브러리를 불러와 카이제곱 수치를 계산한다.
p_values = pd.Series(chi_scores[1],index = X.columns)
p_values.sort_values(ascending = False , inplace = True)
p_values.plot.bar()
이렇게 나온 값으로 카이제곱 통계의 값이 가장 높은 features을 선택하는데 사용가능하다.
Fisher's Score
평균과 분산을 사용하여 피처의 순위를 매기는 필터 방법. 위 방법론의 핵심 아이디어는 선택한 피처가 포함된 데이터 공간에서 서로 다른 클래스의 데이터 포인트 간 거리가 최대한 크고 같은 클래스의 데이터 포인트 간 거리가 최대한 작도록 피처의 하위 집합을 찾는 것이다. (Gu, Quanquan, Zhenhui Li, and Jiawei Han. "Generalized fisher score for feature selection." arXiv preprint arXiv:1202.3725 (2012).)
예를 들어 입력데이터(행렬 $ X \in R^{d \times n} $)가 있을 때 m개의 특징을 선택한다고 한다면 행렬은 $ Z \in R^{m \times n} $으로 감소한다. 이때 fisher score는

이렇게 계산된다. 이때 γ는 양의 정규화 파라미터이고, $ \tilde{S}_b $는 클래스 간 산점도 행렬이라고 하며, $ \tilde{S}_t $는 총 산점도 행렬을 의미한다.

$ \tilde{ \mu }_k $와 $n_k$는 축소된 데이터 공간에서 각각 k 번째 클래스의 평균 벡터와 크기를 의미한다.
위 식을 이용해 각 기능에 대한 피셔 점수를 계산하여 점수가 높은 상위 순위의 기능을 선택한다. 각 기능의 점수는 독립적으로 계산되기 때문에 휴리스틱 알고리즘에 의해 선택된 기능은 suboptimal하다. 개별 점수는 상대적으로 낮지만 전체적으로 합산하면 점수가 매우 높은 특징이 있을 수 있는데 이를 선택하지 못한다는 단점이 존재한다. 또한 중복된 피처를 처리하지 못한다.
code
from skfeature.function.similarity_based import fisher_score
df = pd.read_csv("pulsar_stars.csv")
X = df.iloc[:, :-1]
y = df.iloc[:, -1]
score = fisher_score.fisher_score(X.to_numpy(), y.to_numpy())skfeature(sklearn이 아니다) 라이브러리에서 불러와서 사용 가능하다.
score = pd.Series(score)
score.index = X.columns
score.sort_values(ascending = False)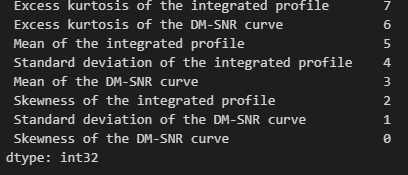
앞에서 해본 IG의 결과랑 비교해보자.


제법 비슷하게 결과가 나온다.
Missing Value Ratio
결측값 처리 과정과 유사하다.
Correlation coefficient
피어슨 상관계수란 연속형 변수의 상관관계 분석으로 -1에서 1사이의 값을 가진다. 상관 관계가 +- 0.8 이상이면 높은 상관관계가 있다고 한다. 변수 간의 상관관계가 높으면 다중공선성 문제가 나타난다.
다중공선성 문제를 해결하는 것에는 VIF 측정 방법도 존재한다.
VIF란 Variance Inflation Factor, 분산확장요인이라고한다. 다중 선형 회귀 모델에서 다중 공선성의 심각도를 측정하는데 이용된다. 독립변수 간에 다중공선성이 있을 때의 분산과 다중공선성이 없을 때의 분산의 비율을 측정하는 것으로 계산되어진다.

VIF 수치가 10 이상이면 다중공선성 문제가 발생한다.
code
pearson_corr= df.corr()
plt.figure(figsize=(50, 50))
# 전체 상관 계수 시각화
sns.heatmap(data = pearson_corr, annot=True, cmap='Blues')전체 상관 계수 시각화하는 코드. 여기서 사용한 상관계수는 피어슨 상관계수를 이용했다.
# VIF를 계산
# VIF 수치가 10 이상이면 다중공선성 문제가 발생
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
def feature_engineering_XbyVIF(X_train):
vif = pd.DataFrame()
vif['VIF_Factor'] = [variance_inflation_factor(X_train.values, i)
for i in range(X_train.shape[1])]
vif['Feature'] = X_train.columns
return vif
vif = feature_engineering_XbyVIF(X_train)
# VIF가 높은 순으로 정렬
vif = vif.sort_values(by='VIF_Factor', ascending=False)
print(vif)참고
Select Features for Machine Learning Model with Mutual Information
Machine Learning models are amazing when trained with an appropriate set of training data. ML models described in the textbook and using datasets from Scikit-learn, sample datasets are already…
towardsdatascience.com
Chi-Square Test for Feature Selection in Machine learning
We always wonder where the Chi-Square test is useful in machine learning and how this test makes difference.Feature selection is an…
towardsdatascience.com
Using the Chi-Squared test for feature selection with implementation
The fewer the features, the easier to interpret the model
towardsdatascience.com
Gu, Quanquan, Zhenhui Li, and Jiawei Han. "Generalized fisher score for feature selection." arXiv preprint arXiv:1202.3725 (2012).
'Machine Learning' 카테고리의 다른 글
| [ML/데이터 전처리]Feature Selection - Embedded (0) | 2023.06.30 |
|---|---|
| [ML/데이터 전처리]Feature Selection - Wrapper (0) | 2023.06.29 |
| [ML/DL] manifold? (0) | 2023.02.21 |
| [ML] Dimensionality Reduction #2 t-SNE, LLE (1) | 2023.02.03 |
| [ML] Dimensionality Reduction #1 PCA, LDA (0) | 2023.02.03 |
소중한 공감 감사합니다