[ML] Dimensionality Reduction #2 t-SNE, LLE

t-SNE(t-distributed stochastic neighbor embedding)

높은 차원의 복잡한 데이터를 2차원에 차원축소하는 방법이다. 고차원 공간에서 유사한 두 벡터가 저차원에서도 유사하도록 원공간에서 점들 간의 유사도를 보존하며 차원을 축소한다. 시각화에 주로 사용하며 대표적으로 워드 임베딩을 시각화할 때 사용된다. 이전에 소개한 PCA, LDA와 달리 비선형적인 차원 축소 방법이다.

이미지 출처: https://towardsdatascience.com/t-sne-machine-learning-algorithm-a-great-tool-for-dimensionality-reduction-in-python-ec01552f1a1e

t-SNE에 대해 자세히 알아보기 위해 먼저 이름의 뜻부터 살펴보도록하자.

t-distributed: t-분포를 따른다.
stochastic: 반복 프로세스에서 무작위로 선정
neighbor: 관심 있는 데이터 지점 근처에 위치하는 데이터 지점
embedding: 임베딩. 고차원에서 저차원으로 만든다.

 

위 정의를 종합해보면 t-SNE는 이웃한 점에 대한 정보를 보존하며 고차원 공간에서의 점들의 유사성과 그에 해당하는 저차원 공간에서의 점들의 유사성을 계산하여 반복하는 기술이다.

t-SNE의 과정

t-SNE는 포인트들 사이의 거리에 기반해 점들의 "유사성"을 결정한다. 가까운 점은 "비슷한" 것으로 간주되고, 먼 점은 "비슷한" 것으로 간주된다. 그 계산 과정은 다음과 같다. 점과 이웃한 점의 거리를 측정한 후 정규 곡선에 배치한다. 모든 점에 대해 해당 작업을 실시하며 지역의 밀도변화를 고려해 약간의 스케일링을 적용한다.

이후 모든 점들을 저차원 공간에 무작위로 매핑하고 위 과정에서 설명한 것과 같은 점 사이의 "유사성"을 계산한다. 단 이번에는 정규분포가 아닌 t-분포를 사용한다. 이렇게 만들어진 분포는 당연하게도 원래의 행렬과 닮지 않았다. 따라서 위 작업을 반복적으로 하며 원래 행렬과 비슷하게 만든다. 각 반복을 진행할 수록 점은 원래의 고차원 공간에서 멀리 떨어진 "가장 가까운 이웃"을 향해 이동한다.

이 작업을 최대 반복 횟수에 도달하거나 더 이상 개선할 수 없을 때까지 계속한다. 이 과정을 다르게 표현하자면 gradient descent 방식을 사용하여 전체 데이터 포인트의 KL-divergence 합계를 최소화한다.

KL-divergence: 한 확률 분포가 두 번째 예상 확률 분포와 어떻게 다른지 측정하는 척도

t-SNE에서 t-분포를 사용한 이유

 정규 분포는 꼬리가 두텁지 않아서 i번째 개체에서 적당히 떨어져 있는 이웃 j와 아주 많이 떨어져 있는 이웃 k가 선택될 확률이 크게 차이가 나지 않게 된다. 따라서 높은 차원 공간에서는 분포의 중심에서 먼 부분의 데이터 비중이 높기 때문에 데이터 일부분의 정보를 고차원에서 유지하기 어렵다. t-분포에서는 일반적인 정규분포보다 끝단의 값이 두터운 분포를 가지기 때문에 이를 방지할 수 있고 따라서 t-분포를 사용한다.

t-SNE에서 유의해야하는 점

t-SNE는 차원축소에 대한 비모수적 접근법(어떠한 parameter를 사용하지 않거나 매우 제한된 조건을 사용하여 원하는 결과를 얻는 과정)이기 때문에 비모수적 접근법이 가지는 단점을 가진다.랜덤 초기화 및 확률적 특성 때문에 각 실행 후에 다른 결과를 얻을 수 있다. 재현하기 위해서는 시드(random_state)를 지정이 필요하다.

t-SNE 알고리즘

1. 모든 i, j 쌍에 대하여 $x_i$,$x_j$의 유사도를 가우시안 분포를 이용해 나타낸다
2. $x_i$와 같은 개수의 점 $y_i$를 낮은 차원 공간에 무작위로 배치하고, 모든 i, j 쌍에 관하여 $y_i$, $y_j$의 유사도를 t-SNE를 이용해 나타냄
3. 앞의 1, 2에서 정의한 유사도 분포가 가능하면 같아지도록 데이터 포인트 $y_i$를 갱신
4. 수렴 조건까지 과정 3을 반복

t-SNE의 구현

 

비교를 위해 PCA와 LDA 사용

from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt

digits = load_digits()

fig, axes = plt.subplots(2,5,figsize=(10,5),
                        subplot_kw = {'xticks':(), 'yticks':()})
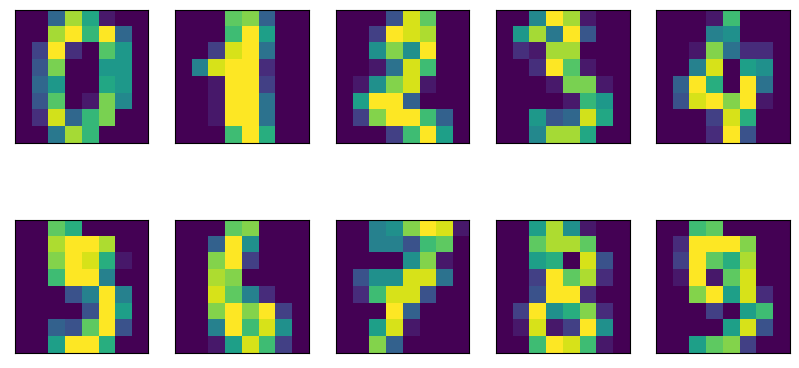
for ax, imgs in zip(axes.ravel(), digits.images):
    ax.imshow(imgs)

MNIST 손글씨 분류 데이터 사용

# PCA, LDA 사용

# 차원 축소: 2차원
n_components = 2
tsne = TSNE(n_components=n_components)

#비교를 위한 PCA, LDA
pca = PCA(n_components=n_components)
lda = LinearDiscriminantAnalysis(solver='svd')

scaler = StandardScaler()
scaler.fit(digits.data)
digits_scaled = scaler.transform(digits.data)

# PCA
pca.fit(digits.data)

digits_pca = pca.transform(digits_scaled)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525",
          "#A83683", "#4E655E", "#853541", "#3A3120","#535D8E"]
plt.figure(figsize=(10,10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max())
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max())
for i in range(len(digits_scaled)):
    plt.text(digits_pca[i, 0], digits_pca[i,1], str(digits.target[i]),
            color = colors[digits.target[i]], fontdict={'weight': 'bold', 'size':9})
plt.title("PCA")
plt.xlabel("pca_component 1")
plt.ylabel("pca_component 2")

#LDA
lda.fit(digits_scaled, digits.target)
digits_lda = lda.transform(digits_scaled)


plt.figure(figsize=(10,10))
plt.xlim(digits_lda[:, 0].min(), digits_lda[:, 0].max())
plt.ylim(digits_lda[:, 1].min(), digits_lda[:, 1].max())
for i in range(len(digits_scaled)):
    plt.text(digits_lda[i, 0], digits_lda[i,1], str(digits.target[i]),
            color = colors[digits.target[i]], fontdict={'weight': 'bold', 'size':9})
plt.title("LDA")

# t-SNE

digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10,10))
plt.xlim(digits_tsne[:,0].min(), digits_tsne[:,0].max()+1)
plt.ylim(digits_tsne[:,1].min(), digits_tsne[:,1].max()+1)
for i in range(len(digits.data)):
    plt.text(digits_tsne[i,0], digits_tsne[i,1], str(digits.target[i]),
            color = colors[digits.target[i]],
            fontdict = {'weight':'bold','size':9})
plt.xlabel("t-SNE 특성 0")
plt.ylabel("t-SNE 특성 1")
plt.title("t-SNE")

LLE(Locally Linear Embedding, 지역적 선형 임베딩)

Nonlinear Dimensionality Reduction by Locally Linear Ebedding (Roweis et.al) 논문에서 제안된 알고리즘으로  입력 데이터셋을 낮은 차원의 단일 글로벌 좌표계(single global coordinate system)으로 매핑하여 차원을 축소하는 알고리즘이다.

데이터 포인트들이 k개의 neighbor들과 얼마나 선형적으로 연결되어있는가를 추론하며 특정 개체를 잘 표현하는 이웃들의 가중치를 찾는 것이 목적이다. 앞에서 살펴본 t-SNE와 같이 비선형 차원 축소 기법으로 비지도학습이다.

LLE를 사용하면 지역 최적점(Local optimum)에 빠지지 않을 수 있다는 장점을 가진다. 또 사용하기 간단하다. LLE에서 사용되는 가중치와 벡터는 선형대수의 방법으로 계산되지만 점들이 이웃 점들에게서만 재구축된다는 조건은 비선형 임베딩 결과를 초래한다는 것이 특징이다.

LLE 알고리즘

Step 1: Select neighbors
n차원을 가지는 m개의 데이터셋의 각 데이터 포인트에 대해 가장 가까운 이웃을 k개 찾는다.

Step 2: Reconstruct with linear weights
데이터 포인트와 그의 이웃점은 매니폴드의 locally linear patch상에 있거나 가까이 있을거라 가정. 이 가정을 바탕으로 데이터 포인트를 재구성하는 가중치 w를 구한다.

Step 3: Map to embedded coordinates
2에서 구한 가중치 w는 데이터 포인트와 이웃점들 간의 지역 선형 관계를 나타냄. 이러한 관계가 최대한 보존 되도록 데이터를 저차원 공간으로 매핑(mapping)한다.

LLE 코드

make_swiss_roll 데이터 사용

 

비교를 위해 PCA도 사용

from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding

X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=41)

scaler = StandardScaler()
scaler.fit(X)
X_scale = scaler.transform(X)
pca = PCA(n_components=2)
pca_swiss = pca.fit_transform(X_scale)

plt.title("PCA", fontsize=14)
plt.scatter(pca_swiss[:, 0], pca_swiss[:, 1], c=t, cmap=plt.cm.hot)
plt.grid(True)

plt.show()

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
lle.fit(X)

X_reduced = lle.transform(X)

plt.title("LLE", fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18)
plt.axis([-0.065, 0.055, -0.1, 0.12])
plt.grid(True)

plt.show()