[ML] Dimensionality Reduction #1 PCA, LDA
- -
Curse of dimensionality(차원의 저주)

일반적으로 차원이 증가할 수록 데이터 포인트 간의 거리가 기하급수적으로 멀어진다. 즉, 희소한 구조(sparse)를 가지게 되고 공간의 성김이 생기게 된다. 위 그림에서 볼 수 있다시피 1차원에서 보이는 점들의 거리가 차원이 늘어날수록 멀어지는 모습을 볼 수 있다.
이런 현상이 일어나게 될 경우, 위와 같은 데이터로 학습 시켰을 때 예측 정확도가 떨어지는 현상이 나타난다. 이런 현상은 거리기반의 모델인 KNN에서 특히 치명적이다.
Dimensionality Reduction(차원 축소)
고차원, 즉 데이터의 피처가 많으면 차원의 저주 뿐만 아니라 개별 피처 간에 상관관계가 높기 때문에 선형 모델(대표적으로 linear regression)에서 다중 공선성 문제가 발생하게되고 모델의 성능이 떨어진다.
다중 공선성: 독립변수의 일부가 다른 독립변수의 결합으로 표현될 수 있는 경우
해당 문제를 해결하고나 고안된 방법이 차원축소이다. 고차원의 원본 데이터의 의미 있는 특성을 원래의 차원에 가깝게 유지할 수 있도록 하면서 저차원으로 데이터를 변환시킨다. 학습 데이터의 크기를 줄여 학습에 필요한 처리 능력도 줄이는데 여기서 학습 데이터의 크기를 줄인다는 말은 학습 데이터의 양을 줄인다는 것이 아니라는 것이 중요하다.
차원 축소는 피처 선택(feature selection)과 피처 추출(feature extraction)으로 나뉜다. 피처 선택은 특정 피처에 종속성이 강한 피처를 제거하는 것이고 피처 추출은 기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것이다.
차원 축소 알고리즘

여기서 선형, 비선형은 어떤 데이터에서 사용하는가를 가리킨다. 대표적인 차원축소 방법인 PCA는 선형 데이터에서만 사용 가능하다.
PCA(Principal Component Analysis, 주성분분석)
대표적인 차원축소 방법으로 비지도학습이다. 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소한다. 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축으로 차원을 축소하는데 분산이 데이터의 특성을 가장 잘 나타낸다고 간주한다.
PCA 원리
- 데이터 변동성(variance)을 기반으로 첫번째 벡터 축 생성
- 위 벡터 축에 직각이 되는 벡터(직교벡터)를 두번째 벡터 축 생성
- 다시 두번째 벡터 축에 직각이 되는 벡터를 설정하여 세번째 벡터 축 생성
- 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축의 개수만큼의 차원으로 원본 데이터가 차원축소
Linear Algebra에서 PCA
- nxm 행렬 A가 있을 때 A_0 의 각 행을 따라 평균을 구한다.
- 각 행의 m개의 성분에서 평균을 빼면 행렬 A의 각 행의 평균은 0, A의 열은 R^m에서 n개의 점이 됨
- n개의 열벡터의 합은 0, 이렇게 센터링된 행렬을 mean-centered 행렬이라고 함
- n개의 점은 하나의 직선(혹은 평면, R^m의 낮은 차원 부분 공간)에 모여있음
- (0,0)을 지나는 가장 가까운 직선 -> A의 첫번째 특이벡터의 방향
- 입력 데이터의 공분산 행렬을 고유값 분해하고, 고유벡터에 입력 데이터를 선형 변환
PCA 알고리즘
- 입력 데이터 행렬 X의 empirical mean을 계산한 후 모든 데이터에서 평균을 빼줌
- 만들어진 데이터 X’의 가장 큰 singular value부터 k번째 큰 singular value까지에 대응하는 singular vector를 계산
- 뽑아낸 k개의 singular vector로 U를 구성하고 return
PCA 코드
from sklearn.datasets import load_iris
from scipy.linalg import svd
import numpy as np
iris = load_iris().data
n = len(iris) # 행의 개수
p = len(iris[0]) #열의 개수
print(n, p)
# 센터링
iris_ctr = np.zeros((n, p))
iris_ctr = iris - np.mean(iris, axis=0)
U, S, V = svd(iris_ctr, full_matrices=False)
# S는 고유값
# U, V는 고유벡터
iris_pca1 = U*S
iris_pca1 = iris_pca1[:, :2]SVD를 사용한 코드
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
iris_pca2 = pca.fit_transform(iris_ctr)
print(pca.fit_transform(iris_ctr))PCA 라이브러리 사용
import pandas as pd
import matplotlib.pyplot as plt
iris_DF_pca1 = pd.DataFrame(iris_pca1)
iris_DF_pca2 = pd.DataFrame(iris_pca2)
iris_DF_pca1['target'] = load_iris().target
iris_DF_pca2['target'] = load_iris().target
markers= ['^', 's', 'o']
for i, marker in enumerate(markers):
x_axis_data = iris_DF_pca1[iris_DF_pca1['target']==i][0]
y_axis_data = iris_DF_pca1[iris_DF_pca1['target']==i][1]
plt.scatter(x_axis_data, y_axis_data, marker=marker, label=load_iris().target_names[i])
plt.legend()
plt.xlabel('pca_component 1')
plt.ylabel('pca_component 2')
plt.show()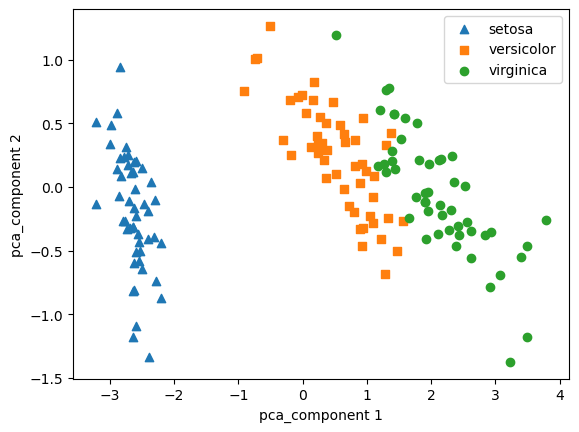
markers= ['^', 's', 'o']
for i, marker in enumerate(markers):
x_axis_data = iris_DF_pca2[iris_DF_pca2['target']==i][0]
y_axis_data = iris_DF_pca2[iris_DF_pca2['target']==i][1]
plt.scatter(x_axis_data, y_axis_data, marker=marker, label=load_iris().target_names[i])
plt.legend()
plt.xlabel('pca_component 1')
plt.ylabel('pca_component 2')
plt.show()

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
rfc = RandomForestClassifier(random_state=156)
scores1 = cross_val_score(rfc, iris_DF_pca1[[0, 1]], load_iris().target, scoring='accuracy', cv=3)
print('PCA 변환 데이터 교차 검증 개별 정확도: ', scores1)
print('PCA 변환 데이터 평균 정확도: ', np.mean(scores1))
scores2 = cross_val_score(rfc, iris_DF_pca2[[0, 1]], load_iris().target, scoring='accuracy', cv=3)
print('PCA 변환 데이터 교차 검증 개별 정확도: ', scores2)
print('PCA 변환 데이터 평균 정확도: ', np.mean(scores2))RandomForestClassifier를 이용해 예측 성능 검증


LDA(Linear Discriminant Analysis, 선형 판별 분석법)
PCA에서는 입력 데이터의 변동성(분산)이 가장 큰 축을 찾는다면 LDA에서는 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾는다.
LDA의 원리
projection 시킨 데이터들에서 같은 클래스에 속하는 데이터들의 variance는 최대한 줄이고 각 데이터들의 평균 값들의 variance는 최대한 키워서 클래스들끼리 최대한 멀리 떨어지게 만든다. 클래스 내부의 분산이 작아진다는 것은 하나의 클래스끼리 잘 모여있다는 의미가 된다.
LDA 알고리즘
- 클래스 내부와 클래스 간 분산 행렬을 구함
- 이 두 개의 행렬은 입력 데이터의 결정 값 클래스별로 개별 피처의 평균 벡터를 구함
- 클래스 내부 분산 행렬을 $S_w$, 클래스 간 분산 행렬을 $S_n$ 이라고 하면 두 행렬을 고유벡터로 분해
- 고유값이 가장 큰 순으로 K개(LDA 변환 차수만큼) 추출
- 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환
LDA 코드
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# x, y 데이터 생성
x, y = make_classification(n_samples=400, n_features=2, n_informative=1, n_redundant=0,
n_clusters_per_class=1, n_classes=2, random_state=42)
# train, test 데이터 분리
train_input, test_input, train_target, test_target = train_test_split(x, y, random_state=40)
# standardization
scaler = StandardScaler()
scaler.fit(train_input)
train_scaled = scaler.transform(train_input)
test_scaled = scaler.transform(test_input)
lda = LinearDiscriminantAnalysis(solver='svd')
lda.fit(train_scaled, train_target)
train_lda = lda.transform(train_scaled)
test_lda = lda.transform(test_input)
# dimension 확인
print(train_lda.shape, test_lda.shape)
slope = lda.coef_[0,1] / lda.coef_[0,0]
t = np.arange(np.min(x[:,0]), np.max(x[:,0]), 0.1)
label0 = y==0
label1 = y==1
# plt.subplot(1,3,1)
plt.plot(t, slope*t, color='red')
plt.scatter(x[label0,0], x[label0,1])
plt.scatter(x[label1,0], x[label1,1])
plt.xlim(np.min(x[:,0])-0.1, np.max(x[:,0])+0.1)
plt.ylim(np.min(x[:,1])-0.1, np.max(x[:,1])+0.1)
plt.xlabel('feature #1')
plt.ylabel('feature #2')
plt.legend(labels=['w', 'class 0', 'class 1'])
plt.title('before transform')
plt.figure()
plt.hist(train_lda[train_target==0], 100)
plt.hist(train_lda[train_target==1], 100)
plt.title('train data')
plt.figure()
plt.hist(test_lda[test_target==0], 100)
plt.hist(test_lda[test_target==1], 100)
plt.title('test data')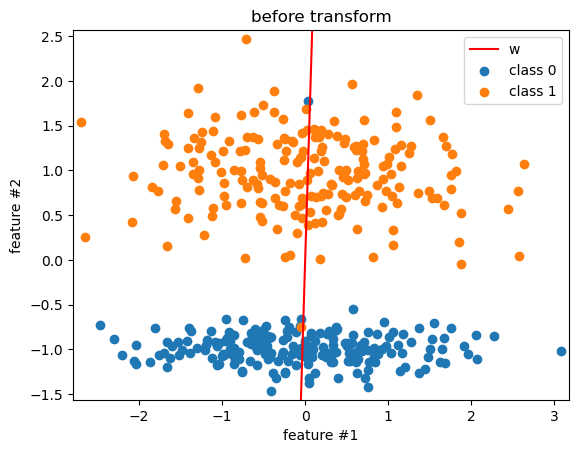


PCA와 LDA에서 주의해야하는 점
데이터의 스케일링이 필요하다. 여러 속성의 값을 연산해야하므로 속성의 스케일에 영향을 받는다. 모든 특성의 범위(또는 분포)를 같게 만들어줘야 제대로 작동한다.
'Machine Learning' 카테고리의 다른 글
| [ML/DL] manifold? (0) | 2023.02.21 |
|---|---|
| [ML] Dimensionality Reduction #2 t-SNE, LLE (1) | 2023.02.03 |
| [선형대수학] 특이값 분해 (SVD, Singular Value Decomposition) (0) | 2023.01.25 |
| [선형대수학] 고유값, 고유벡터, 고유값 분해 (3) | 2023.01.19 |
| [머신러닝] 이상치 탐지(anomaly detection) #03 Local Outlier Factor (0) | 2022.09.08 |
소중한 공감 감사합니다