[선형대수학] 고유값, 고유벡터, 고유값 분해

고유벡터(eigenvector), 고유값(eigenvalue)

고유벡터: 행렬 A를 선형변환으로 봤을 때, 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터
고유값: 위에서 말한 상수배 값

선형변환(linear transformation)
선형 결합을 보존하는, 두 벡터 공간 사이의 함수. 즉 한 점을 한 벡터공간에서 다른 벡터공간으로 이동시키는데 그 이동 규칙을 이야기한다.

즉, n x n 정방행렬 A에 대해 Av = λv를 만족하는 0이 아닌 열벡터 v를 고유벡터, 상수 λ를 고유값이라 정의한다.

정방행렬(square matrix)
같은 수의 행과 열을 가지는 행렬

정방행렬

어떤 행렬은 고유값-고유벡터가 아예 존재하지 않을 수도 있고 어떤 행렬은 하나만 존재하거나 또는 최대 n개까지 존재할 수 있다.

고유값, 고유벡터를 찾는 과정

임의의 n×n 행렬 A에 대하여, 0이 아닌 솔루션 벡터 $\vec{x}$가 존재한다면 숫자 λ 는 행렬 A의 고유값이라고 할 수 있다.

$$A\vec{x} =  \lambda  \vec{x} $$

이때, 솔루션 벡터 $\vec{x}$는 고유값 λ 에 대응하는 고유벡터이다.
위 식은 행렬의 성질에 의해 다음과 같이 바꿀 수 있다.

$$(A- \lambda I) \vec{x}  = 0$$

위 식이 성립하려면 괄호 안의 식이 0이 되거나 $\vec{x}$ = 0이어야 한다. 괄호 안에 있는 식으로 부터 얻는 행렬은 역행렬을 가지지 않아야만 잘못된 solution을 얻지 않는다.

$$det(A- \lambda I)  = 0$$

따라서 이 행렬식을 만족해야한다. 이 행렬식을 특성방정식(Characteristic Equation)이라고도 한다. 행렬식을 통해 고유값을 구하고 그 값을 $A\vec{x} =  \lambda  \vec{x} $에 대입해 고유벡터를 구할 수 있다.

A=[[4, 2], [2, 4]]라는 행렬을 통해 고유값을 구해본 예시이다. 파이썬 라이브러리인 numpy를 통해 고유값과 고유벡터를 구해보면

import numpy as np

#정사각형 배열의 고유값과 우측 고유벡터를 계산
eig = np.linalg.eig
matrix = np.matrix

test = matrix([[4, 2], [2, 4]])
print(eig(test))

value = eig(test)[0]
vector = eig(test)[1]

print("고유값: ", value)
print("고유벡터: ", vector)

결과값: 고유값: [6. 2.] 고유벡터: [[ 0.70710678 -0.70710678] [ 0.70710678 0.70710678]]

같은 고유값이 나오는 것을 확인할 수 있다.

고유값 분해(eigen decomposition)

그렇다면 고유값 분해란 무엇일까? 행렬을 정형화된 형태로 분해함으로써 행렬의 고유값 및 고유벡터로 표현하는 것이다. 

위 개념을 알기 위해서는 행렬의 닮음에 대해서도 알아야한다.

행렬의 닮음?

모든 가역행렬 B에 대하여 $BAB^{-1}$의 고유값은 A의 고유값과 같다. A의 고유벡터 $\vec{x}$는 B를 곱한 $B\vec{x}$의 형태로 $BAB^{-1}$의 고유벡터가 된다. 이 아이디어는 크기가 큰 행렬의 고유값을 계산할 때 사용한다. 

가역행렬(invertible matrix)
역행렬이 존재하는 행렬. 역행렬이 존재하기 위해서는 행렬식이 0이 되면 안된다.

여기서 $B=P^{T}AP$을 만족하는 직교행렬 P가 존재할 때, B는 A에 직교닮음(orthogonally similar)라고 한다.

직교행렬(Orthogonal Matrix)
행벡터와 열벡터가 유클리드 공간의 정규 직교 기저를 이루는 실수 행렬. 
직교행렬의 역행렬은 직교행렬 자신의 전치행렬(transpose matrix)와 같다

직교행렬

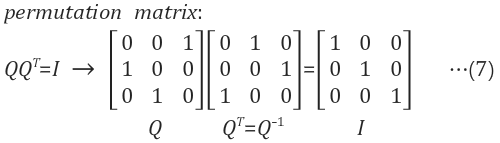
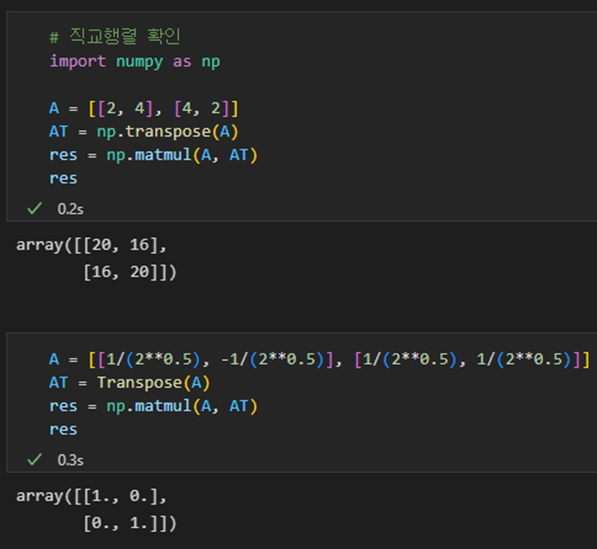
# 직교행렬 확인
import numpy as np

A = [[2, 4], [4, 2]]
AT = np.transpose(A)
res = np.matmul(A, AT)
# 직교행렬이 아님
'''array([[20, 16],
       [16, 20]])'''
       
A = [[1/(2**0.5), -1/(2**0.5)], [1/(2**0.5), 1/(2**0.5)]]
AT = Transpose(A)
res = np.matmul(A, AT)
res

#직교행렬임
'''
array([[1., 0.],
       [0., 1.]])
'''

직교(Orthogonal)

직교란 선형대수를 공부하다보면 흔히 볼 수 있는 용어로, 수직을 뜻한다. 이는 선형대수에서 두 벡터 사이의 각도라는 의미 이상으로 확장된다.

1. 서로 직교인 벡터 x와 y: $x^Ty=x_1y_1 + ... + x_ny_n = 0$을 통해 판정한다.
   x와 y가 복소 성분을 포함하는 경우, ${\bar{x}^T}y={\bar{x}_1}y_1+...+{\bar{x}_n}y_n$으로 바꾸어 판정
2. 부분 공간의 대한 직교 기저: 모든 벡터 쌍은 $v^T_iv_j = 0$를 만족한다.
   정규직교기저: 단위벡터($v^T_iv_i = 1$, 즉 길이가 1)인 직교 기저를 의미한다.
   직교기저를 정규직교기저로 만드려면 모든 기저벡터 $v_i$를 자신의 크기($\parallel v_i \parallel$)로 나눈다
3. 직교 부분공간(Orthogonal subspace) R와 N: 공간 R의 모든 벡터는 N의 모든 벡터와 정규 직교한다
   => 행공간과 영공간은 직교한다
4. 정규직교인 열을 가지는 길고 얇은 행렬 Q: $Q^TQ=I$를 만족한다.
   Q에 어떤 벡터 x를 곱하더라도 x의 길이는 변하지 않는다.
   $$(Qx)^T(Qx) = x^TQ^Tx = x^Tx$$
   이므로 $ \parallel Qx \parallel  =  \parallel x \parallel $가 성립한다.
   m>n일 때, m개의 행은 $R^n$ 위에서 정규직교하지 않는다.
5. 직교행렬은 정규직교인 열이 있는 정사각행렬로 $Q^T = Q^{-1}$가 성립한다.
   $Q^TQ = I$인 정사각행렬은 $QQ^T = I$도 만족한다. 정사각행렬 Q에 대하여 좌역행렬(left inverse) $Q^T$는 Q의 우역행렬(right inverse)이다. nXn 행렬의 직교인 열들은 $R^n$의 정규직교기저가 된다. Q의 행들도 $R^n$의 정규직교기저이다.
   직교 행렬이라는 말은 실제로는 정규직교행렬을 말한다.

직교 대각화(Orthogonal Diagonalization)

정사각행렬 B가 대각행렬 D라면 위 식을 $D=P^{T}AP$ 이렇게 쓸 수 있다. 이때 직교행렬 P는 A를 ‘직교 대각화’ 한다고 말하며, A는 ‘직교 대각화 가능(orthogonally diagonalizable)’하다고 한다.

* 직교 대각화(Orthogonal Diagonalization) 가능 조건

• 행렬 A의 고유 벡터는 n개의 정규 직교 벡터를 만족한다
• 행렬 A가 직교 대각화 가능하려면 A는 반드시 대칭 행렬이어야 한다
  • 대표적인 대칭행렬로는 공분산 행렬이 존재한다.

고유값 분해(eigen decomposition)

직교대각화의 한 종류로 스펙트럼 분해라고도 한다. 행렬을 고유 벡터, 고유값의 곱으로 분해하는 것이다.

λ는 A의 고유값 u는 고유벡터

$$A=PDP^{T}$$

Power Iteration

Power Iteration 또는 Power method라고도 하며 고유값 분해를 위한 알고리즘 중 하나이다. 

$$ Av= \lambda v $$

라는 식이 있다고 하자. 이때 고유벡터와 고유값은 행렬 A의 차원의 개수(n)만큼 나온다. 고유값의 절대값이 큰 것부터 순차 번호를 매기고, 각 고유값에 해당하는 고유벡터도 동일한 순서대로 나열한다.

그럼 다음과 같은 식으로 나타낼 수 있다.

$$X = x_1v_1 +x_2v_2+ ... +x_nv_n$$

$$AX =  \lambda _1x_1v_1 +\lambda _2x_2v_2+ ... +\lambda _nx_nv_n$$

위 식에서 A를 k번 곱하게 되면

$$AX =  \lambda^k _1x_1v_1 +\lambda^k _2x_2v_2+ ... +\lambda^k _nx_nv_n$$

$$A^kX =  \lambda^k _1[x_1v_1 +(\frac{\lambda _2 }{\lambda _1})^kx_2v_2+ ... +(\frac{\lambda _n }{\lambda _1})^kx_nv_n]$$

첫번째 고유값의 절대값이 항상 다른 고유값의 절대값보다 크다고 정의했으므로, k를 무한대로 보내면, 위의 수식에서 괄호의 첫번째 항만 제외하고 다른 항들은 모두 0으로 수렴한다

$$\lim_{k \rightarrow  \infty } A^kX =  \lambda ^k_1x_1v_1$$

Power Iteration Algorithm

1.벡터 x를 임의로 선택한다.

2.y = Ax

3.y를 정규화(크기를 1로 만듦)을 시킨다.

4.y와 x가 같으면(원하는 정밀도까지) y가 고유 벡터이므로 6번으로

5.x를 y로 치환하고 2번으로

6. Ax와 x를 비교하여 고유값을 구한다

def eigenvalue(A, v):
    Av = A.dot(v)
    return v.dot(Av)

def power_iteration(A):
    # 배열의 형태 확인
    n, d = A.shape
    
    #임의의 벡터 선택
    v = np.ones(d) / np.sqrt(d)
    ev = eigenvalue(A, v)

    while True:
        Av = A.dot(v)
        #정규화
        v_new = Av / np.linalg.norm(Av)

        ev_new = eigenvalue(A, v_new)
        # 고유 벡터 확인
        if np.abs(ev - ev_new) < 0.01:
            break

        v = v_new
        ev = ev_new

    return ev_new, v_new

Power Iteration은 PCA(주성분분석), Stochastic Matrices(마르코프 행렬), Pagerank에서 사용된다.